V/ Leistungsfähigkeit und spektrale Empfindlichkeit von Cu(In,Ga)Se2 - Solarmodulen
    In den meisten der heute verwendeten Solarmodulen wird Silizium als Halbleiter eingesetzt. Mono- oder polykristalline Zellen erreichen zwar hohe Wirkungsgrade (15-2O%), sind dafür aber sehr teuer in der Herstellung. Dünnschicht-Silizium-Solarzellen sind wesentlich günstiger, bringen jedoch nur 5-7% Wirkungsgrad. Wird statt Silizium der Halbleiter Kupfer - Indium - Gallium - Diselenid (CIGS) verwendet, können Solarmodule in Dünnschichttechnologie hergestellt werden, die höhere Wirkungsgrade erreichen.
Rendement et sélectivité spectrale de modules solaires
    La plupart des modules solaires utilisés actuellement sont équipés de semi-conducteurs au silicium. Les rendements des cellules mono ou polycristallines sont, il est vrai, élevés, mais leur fabrication est par contre fort coûteuse. Des cellules solaires recouvertes de couches ultraminces de silicium, bien qu’etant nettement plus avantageuses, n’ont cependant un rendement que de 5 à 7%. Il est toutefois possible d’obtenir de meilleurs rendements en utilisant des couches ultraminces an cuivre-indium-gallium-diselenid (CIGS) plutôt qu’au silicium comme semi-conducteurs pour fabriquer des modules solaires.
Markus Leutwyler und Wilhelm Durisch
Dünnschicht-Solarmodule mit höheren Wirkungsgraden
Dem Team von Bernhard Dimmler am Zentrum für Sonnenenergie- und Wasserstoff-Forschung (ZSW) in Stuttgart ist es bereits 1998 gelungen, CIGS-Dünnschicht-Solarmodule von 30x30 cm2 mit einem Wirkungsgrad von etwa 12% zu produzieren [1]. Kleine Zellen erreichen gar über 17%. Am Paul Scherrer Institut PSI ist nun ein CIGS-Modul des 75W (30x30 cm2, 41 einzelne Zellen) unter Realbedingungen getestet worden. Dort ist auf dem Dach eines Gebäudes eine entsprechende Testanlage installiert [2]. Unter freiem Himmel steht ein Sun-Tracker, auf dem die Prüflinge fixiert werden (Bild 1):

Bild 1 Sun-Tracker auf Gebäudedach am PSI
Der Sun-Tracker folgt fortlaufend dem Sonnenstand, so dass die Sonne immer senkrecht auf das Modul scheint. Über dicke Kabel wird der vom Modul produzierte Strom ins Laborgebäude geführt, wo computergesteuert Kennlinien aufgenommen werden. Zusätzlich zu den elektrischen Daten des Moduls wird mit Pyranometern die Globalstrahlung gemessen. Aus der elektrischen Leistung des Moduls, der Globalstrahlung und der Fläche des Moduls, kann nun der Wirkungsgrad berechnet werden.

Wirkungsgrad unter Standard-Testbedingungen
    Der Wirkungsgrad einer Solarzelle sinkt mit steigender Temperatur, wobei nahezu eine lineare Beziehung zwischen Temperatur und Wirkungsgrad besteht. Um Solarzellen miteinander vergleichen zu können, wird der Wirkungsgrad immer auf die Standard-Temperatur von 25 0C bezogen angegeben. StandardTestbedingungen liegen dann vor, wenn die Einstrahlung bei 1000 W/m2 und die relative atmosphärische Masse (AM) bei 1,5 liegt. Unsere Messungen fanden im Spätsommer um die Mittagszeit statt. Standardbedingungen herrschten in guter Annäherung.
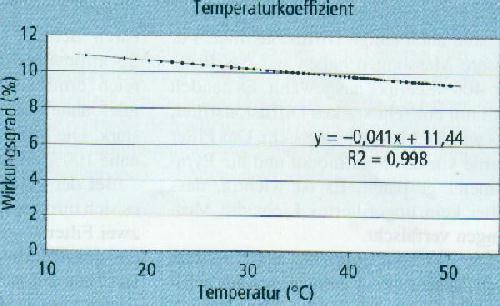
    Wird ein Solarmodul der Sonne ausgesetzt, erwärmt sich die Halbleiterschicht auf Temperaturen über 60 0C. Allerdings benötigt dieser Erwärmungsprozess eine gewisse Zeit. Dies ist bei der PSI-Testanlage die Grundlage für die Messung des Temperaturkoeffizienten. Während der Erwärmungsphase werden laufend Messungen gemacht. Wird nun die gemessene Temperatur dem entsprechenden Wirkungsgrad gegenübergestellt, kann der Temperaturkoeffizient mit einer linearen Regression bestimmt werden. Für das CIGS-Modul des ZSW haben wir einen Wirkungsgrad von 10.4% und einen Temperaturkoeffizienten von -0,041%/0C ermittelt. Je 100C Erwärmung sinkt der Wirkungsgrad also um 0,4%-Punkte, bei 60 0C liegt er nur noch bei 9%. Die abgegebene elektrische Leistung beträgt somit nur noch 86% des Standardwerts. Dies zeigt die enorme Bedeutung des Temperaturkoeffizienten (Bild 2).


Bild 2 Temperaturkoeffizient
Bei amorpben Siliziumzellen liegt der Temperaturkoeffizient bei etwa -0,01%10C (z.B. Tripelzelle von UniSolar [4]).

Einfluss der Diffusität auf den wirkungsgrad
    Es ist anzunehmen, dass gerichtete, senkrecht auf die Oberfläche des Solarmoduls eintreffende Sonnenstrahlung einen höheren Wirkungsgrad erzielt als diffus eintreffende mit gleicher Intensität. Sowohl auf der Oberfläche des Trägermaterials (eine Glasscheibe) wie auch auf der Oberfläche des Halbleiters treten Reflexionen des eintreffenden Lichts auf. Diese sind bei senkrechter Einstrahlung am geringsten.
    Die Firma Lee aus England stellt diverse Filterfolien für den Einsatz im Bühnen-, Film- und Videobereich her. Darunter sind auch einige Diffusionsfilter. Für unsere Messungen haben wir das Filter Nr. 400 «Leelux» ausgewählt. Es handelt sich um ein sehr starkes Diffusionsfilter, das wie ein Milchglas aussieht. Das Filter wurde vor das Solarmodul und die Pyranometer gespannt. Es ist wichtig, dass dabei kein ungefiltertes Licht die Messungen verfälscht.
    Der Wirkungsgrad bei ungefiltertem Licht kann nun mit demjenigen bei gefiltertem Licht verglichen werden. Bei unseren Messungen sank er von 10.41% auf 9.51% also auf einen Wert von 91.4% des Ausgangswerts. Die Abnahme betrug somit 8.6%. Allerdings ist dieser Wert kritisch zu betrachten. Bei unseren Messungen war es möglich, dass Licht hinter der Folie hin und her reflektiert wurde und die Pyranometer somit zu viel Licht erhalten haben. Es deutet zwar alles darauf hin dass das Spektrum durch die Filterfolie nicht verändert wird. Dies müsste aber mit einem Spektrometer verifiziert werden, das auch die diffuse Strahlung misst. Des Weiteren könnte der Wirkungsgrad auch durch die verminderte Intensität etwas abgenommen haben (Teillastverhalten).

Ermittlung der spektralen Empfindlichkeit mittels Filtermethode
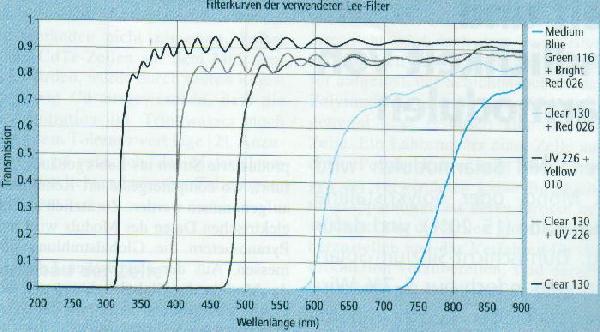
    In welchem Wellenlängenbereich arbeitet das Solarmodul arn effizientesten? Urn dies zu bestimmen, haben wir eine sehr kostengünstige Messmethode entwickelt. Es wurden Farbfilter gesucht, die eine «Cowshelf»-Charakteristik mit einer steilen Flanke aufweisen. Die Wellenlänge des «Cutoffs» soll variieren. Von verschiedenen in Frage kommenden Filtern wurde mit einem Perkin-Elmer-Spektrorneter die Transmission im sichtbaren Bereich und mit einem FFT-IRSpektrometer diejenige im infraroten Bereich ermittelt. Im infraroten Lichtbereich ähneln sich alle gemessenen Filter stark. Die Transmission ist durchgehend nahe 100% (Bild 3):


Bild 3 Transmission im sichtbaren Bereich
    Bei der getroffenen Auswahl handelt es sich um vier Filterkombinationen zu je zwei Filter sowie um das Filter «Clear», das den Blindwert liefert. Bei jeder Filterkombination wird die transmittierte Einstrahlungsleistung sowie die abgegebene elektrische Leistung gemessen. Die Filter werden mit aufsteigendem «Cutoff»-Wert der Wellelänge eingesetzt. Mit jedem neuen Filter wird ein weiterer Bereich des Spektrums weggefiltert. Die Einstrahlungsleistung hinter dem Filter verringert sich. Wird nun die Differenz zwischen den Einstrahlungsleistungen zweier aufeinanderfolgender Filterkombinationen in Relation gesetzt zur Differenz der abgegebenen elektrischen Leistung, so kann daraus der elektrische Wirkungsgrad im entsprechenden Wellenlängenbereich errechnet werden.
    Diese Berechnung ergab folgende Werte.
· 320-400 nm: h = 0,32%
· 400-490 nm: h = 7,3%
· 490-620 nm: h = 14,6%
· 620-8OOnm: h 16,7%
· 800-1000 nm: h = 5.8%
· > l000nm: h =0%
    Die Module sind also besonders im für unsere Augen grünen bis tiefroten Lichtbereich effizient.
    Da bei allen Messungen je zwei Filter zum Einsatz kommen, und aus den gemessenen Werten die Differenz gebildet wird, sind systemische Fehler wie bei der Messung mit dem Diffusfilter viel weniger zu befürchten.

Verhalten des Moduls bei tiefen Einstrahlungswerten
    Unsere Datenlage ist jedoeh zu gering, um den Wirkungsgrad in Abhängigkeit der Einstrahlung zu modellieren. Deshalb sei hier auf die Tabelle 1 verwiesen:


Tabelle I Wirkunsgrad in Abhängigkeit von der Einstrahlung
    Generell lässt sich sagen, dass die getesteten Module auch bei schwachen Einstrahlungen recht effizient arbeiten.

Anwendung des Kennlinien-modelis zur Bestimmung des Serie- und Parallelwiderstandes
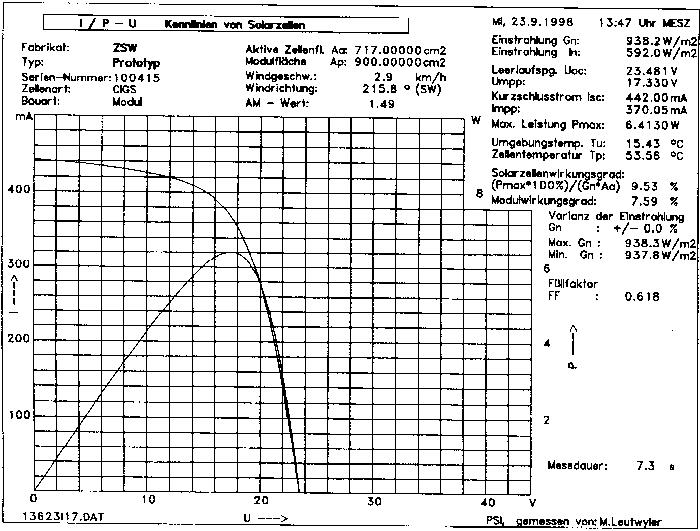
    Die Kennlinie einer Solarzelle (Bild 4) kann mathematisch modelliert werden.


Bild 4 Kennlinie des getesten CIGS-Moduls
Wird das Modell an die gemessenen Daten «gefittet», können die Parameter Serie- und Parallelwiderstand ermittelt werden. Für das Modul mit seinen 41 Zellen ergaben sich folgende Werte:
· Seriewiderstand (Modul): 4,11 W
· Parallelwiderstand (Modul): 584 W
    Diese beiden Widerstände verursachen einen Abfall des Wirkungsgrades. Das zeigt sich auch in der Tatsache, dass der Füllfaktor bei nur 0,618 liegt. Durch eine Optimierung unter anderem des Seriewiderstandes könnte das Modul sicherlich wirkungsgradmässig kleinen Laborzellen angenähert werden.

Folgerungen
    In der Photovoltaik-Freiland-Testanlage des PST [2] gelang es mit relativ geringem Aufwand, einige aufschlussreiche Kenngrössen eines neuartigen Solarzellenmoduls zu ermitteln. Zudem gelang es mit einer sehr einfachen neuen Methode auch den spektralen Wirkungsgrad zu bestimmen. Sein Maximum tritt bei rotem bis tiefrotem Licht auf, was etwas unterhalb der Bandlücken-Wellenlänge der CIGS-Zelle liegt [3]. Es verläuft aber oberhalb des spektralen Intensitätsmaximums des Sonnenlichts, welches unter STC-Bedingungen bei etwa 500 nm liegt. Daraus ergibt sich, dass durch leichte Erhöhung der Bandlückenenergie der Gesamtwirkungsgrad möglicherweise noch etwas gesteigert werden könnte. Verglichen mit kristallinen Siliziumzellell ist der Seriewiderstand hoch. Durch Senkung dieses Werts (besser leitende Elektroden durch Prozessoptimierung) könnte der Wirkungsgrad vielleicht auch noch etwas angehoben werden. Allerdings sollte damit keine allzu grosse Verteuerung der Module verbunden sein. Der Temperaturkoeffizient des Wirkungsgrades liegt mit -0,043%/0Crelativ günstig zwischen jenen amorpher und kristallinen Solarzellen. Der am getesteten CIGS-Modul festgestellte STCWirkungsgrad von 10.4% ist für amorphe Dünnfilmmodule dieser Grösse vergleichsweise hoch. Über allfällige Degradationsprozesse kann aus den bisherigen Messungen keine Aussage gemacht werden.

Literatur
[1] Die neuen CIS-Zellen machen Sonnenstron erschwinglich. Bild der Wissenschaft 5/1998, S. 32-37.
retour au texte
[2] W. Durisch, D. Tille, A. Wörz and W. Plapp: Characterisation of Photovoltaic Generators. Applied Energy 65(2000), S. 273-284.
retour au texte
[3] A. N. Tiwari F.-J. Haug and H. Zogg: Dünnschichtsolarzellen aus Verbindungshalbleiter. Bulletin SEV/VSE 10/98, S. 4549.
retour au texte
[4] W. Durisch, O. Struss and K. Robert: Efficiency of Selected Photovoltaic Modules under Varying Climatic Conditions. Presented at the WREC 2000, Brighton, UK, 1-7 July 2000. To be published in Renewable Energy.
retour au texte
[5] B. Dimmier und Hans-Werner Schock: CIS-Dünnschichtsolarzellen-Technologie. Forschungsverbund Sonnenenergie-Themen 95/96: Photovoltaik 3, 1996, S. 52-59.
[6] Hans-Werner Schock: Grundlagen der Photovoltaik (Teil 4): Dünnschichtsolarzellen aus Verbindungshalbleitern. Photon, 2. Jahrgang, Heft 1,1997, 5. 14-19.

Adressen: Dr. Wilhelm Durish
Angewandte Photovoltaik
Paul Scherrer Institut, PSI
5232 Villigen PSI
E-Mail: Withelm.Durisch@psi.ch

Richard Menner
Zentrum für Sonnenenergie- und Wassenstoffforschung (ZSW)
Hessbruehlstrasse 21C
D-70565 Stuttgart, Germany
E-Mail: richard.menner@zsw-bw.de